"

6.9 Ultimate geotechnical strength of piles subjected to axial compressive load under undrained conditions (α-Method)

The α–Method is used to analytically estimate the short-term axial collapse load Qf of piles installed in fine-grained saturated soils, when undrained loading conditions prevail i.e., before dissipation of excess pore pressures. Calculation of the collapse load with the α–Method is based on total stresses (Total Stress Analysis-TSA).

The ultimate geotechnical strength Qf in terms of force is equal to the sum of the skin friction resistance Qsf and the end-bearing resistance Qb (Figure 6.17):

(6.3) {Q_f} = {Q_{sf}} + {Q_b}

If the self-weight of the pile is not included in the axial load combination provided by the Structural Engineer, it should be subtracted from the pile resistance, as:

(6.4) {Q_f} = {Q_{sf}} + {Q_b} - {W_p}

It must be noted here that the above Eq. 6.4 is rather conservative, because it does not take into account that soil is unloaded during pile construction. It would be reasonable to subtract from the ultimate strength of the pile Qsf + Qb the weight of the pile minus the weight of the excavated soil. It is acknowledged though that this will not have significant impact on the design of piles.

Estimation of the skin friction resistance developing along the pile shaft is based on the simple Coulomb friction concept (Figure 6.17a). Under undrained conditions, the adhesion factor au is used to correlate the undrained shear strength of the soil, Su to the skin friction resistance in terms of stress fsf as:

(6.5) {f_{sf}} = {a_u}{S_u}

Of course, as discussed in Section 5.2.5, the real cohesion of the soil is usually zero, and the term “adhesion” refers merely to the fact that in a total stress analysis the interface friction is calculated independently of the level of normal stress acting on the interface, as pore pressures are not known.

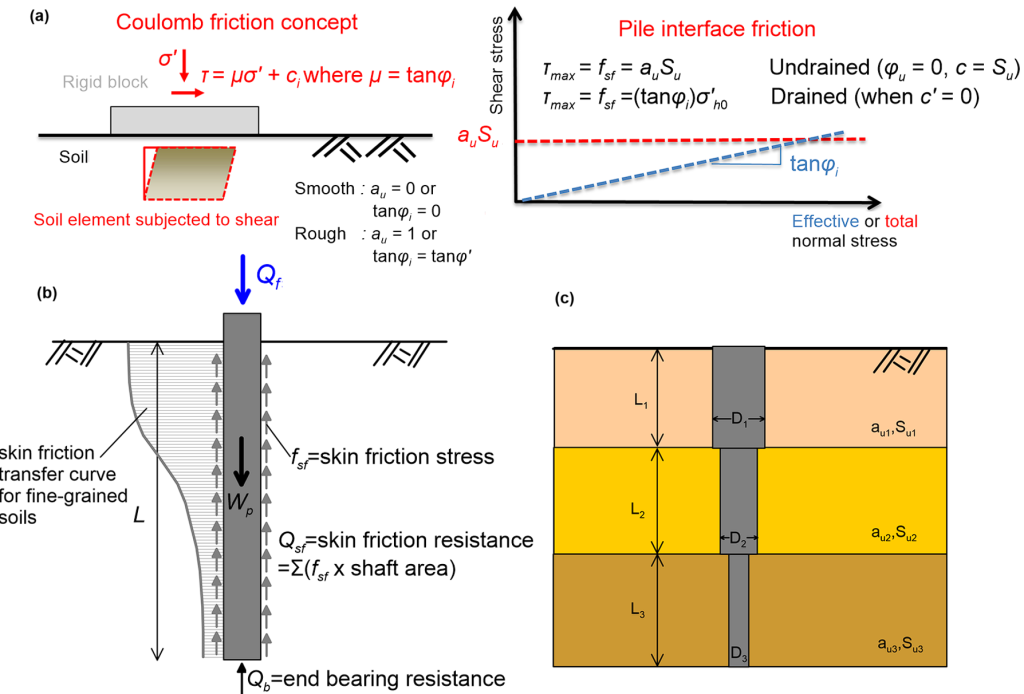
Figure (a) on the top presents a rigid block resting on the surface of soil. A normal compressive stress and a shear stress are applied on the block, and the shear stress is calculated according to Coulomb's friction law. A soil element underneath the block is depicted, and is subjected to shear deformations. Next to that schematic there is a shear stress-normal stress plot, presenting the maximum shear stress predicted by Coulomb's friction law for different stress levels, under drained and undrained conditions. Figure (b) at the bottom left presents a pile of length L subjected to an axial compressive force Qf at its head. The weight of the pile is also depicted as Wp. These loadings are resisted by a force Qb developing at the pile toe, referred to as end bearing resistance, and skin friction stress fsf acting along the pile shaft. The sum of these skin friction stress is referred to as skin friction resistance Qsf. Figure (c) at the bottom right presents a pile of varying diameter, installed in layered soil. Each soil layer features different Su and au properties.
Figure 6.17. (a) Coulomb friction model used to estimate skin friction resistance of piles, (b) Skin friction resistance and end-bearing resistance of a pile subjected to vertical compressive load, and (c) Estimation of the skin friction resistance of a variable-diameter pile embedded in multi-layered soil.

Note that the interface strength generally is taken less or equal to the shear strength of its surrounding soil. While it has been proven experimentally that the strength of specially engineered interfaces can exceed the shear strength of soil, due to the development of a complex failure mode involving passive wedges, it is reasonable to consider that the adhesion factor au cannot exceed au = 1 (rough interface, Figure 6.17a). On the contrary, in the rather theoretical case where the pile-soil interface is perfectly smooth au = 0, and no friction resistance develops. According to the above, the skin friction resistance Qsf (units: force) developing along the embedded length of the pile is calculated as the product of the skin friction stress times the surface area of the pile (Figure 6.17b). Specifically for a cylindrical pile of length L and diameter D in homogeneous soil featuring constant undrained strength Su:

(6.6) {Q_{sf}} = {a_u}{S_u}\pi DL

or, when the undrained strength Su varies with depth z as Su(z):

(6.7) {Q_{sf}} = \int_0^L {\left( {{a_u}{S_u}\left( z \right)\pi D} \right)dz}

In the more general case where a cylindrical pile of variable diameter is embedded in multi-layered soil consisting of n layers (Figure 6.17c), the skin friction resistance must be calculated separately for each soil layer. The sum of the skin friction resistance along each soil layer k will result to the total skin friction resistance of the pile:

(6.8) {Q_{sf}} = \sum\limits_{k = 1}^n {{a_{u,k}}{S_{u,k}}\pi {D_k}{L_k}}

Similarly, two soil sublayers must be considered if the pile diameter changes within the thickness of a soil sublayer with assumed constant undrained shear strength.

According to AS2159, the pile surface area from the ground surface level down to a depth equal to 1.5 pile diameters shall be assumed to be ineffective when estimating the appropriate pile length L values to calculate skin friction resistance, to account for severe soil disturbance during pile driving works.

Various methods have been proposed in the literature to estimate the adhesion factor au with some of the most commonly used ones presented in Figure 6.18a. Additionally, the nomographs proposed by Tomlinson (1987) are presented in Figure 6.18b, which should be conservatively used in the case where the pile toe is founded in a stiff soil layer, overlayed by a very soft clay layer (case (b), Figure 6.18b). Note that the undrained shear strength value Su that will be used to estimate au and the skin friction resistance Qsf must take into account the disturbance of soil around the shaft, as discussed earlier.

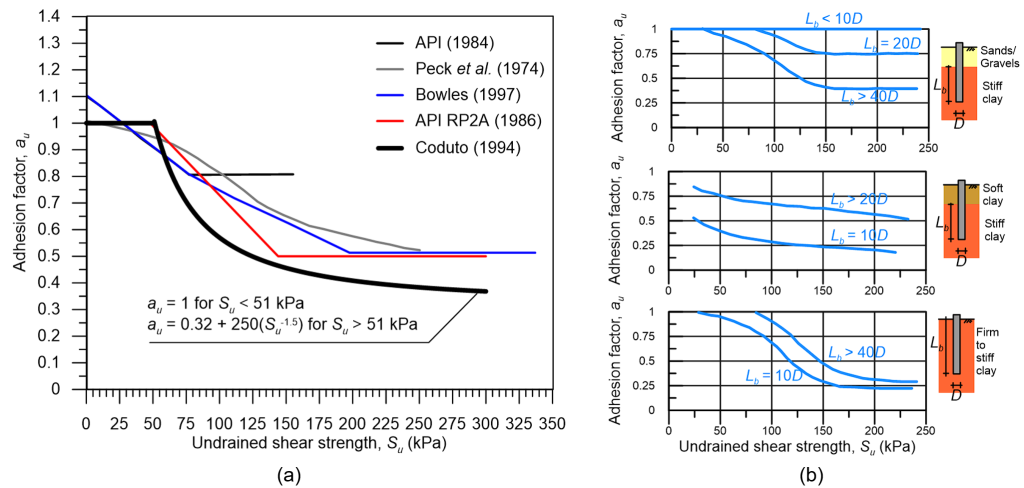
Figure (a) on the left presents the formulas proposed for the variation of the adhesion factor au with the undrained shear strength of soil by API (1984), Peck et al. (1974), Bowles (1997), API RP2A (1986) and Coduto (1994). The later is au = 1 for Su < 51 kPa, au = 0.32+250(Su)^(-1.5) for Su > 51 kPa, and generally provides conservative results. Figurer (b) on the right consists of 3 graphs presenting the variation of the adhesion factor with the undrained shear strength for three different cases: pile installed in sand/gravels underlaid by stiff clay, pile installed in soft clay underlaid by stiff clay, and pile installed in stiff clay. Different curves are presented for different Lb/D values, where Lb is the length of the pile in still clay and D is the pile's diameter.
Figure 6.18. (a) Estimation of the adhesion factor according to API (1984), Peck et al. (1974), Bowles (1997), API (1986) and Coduto (1994), and (b) Estimation of the adhesion factor according to Tomlinson (after Tomlinson 1987).

Notice that the α-method will provide relatively high values of skin friction resistance for piles in soft-to-firm clay (Su < 50 kPa), irrespective of pile roughness, as au depends only on soil’s undrained strength. While there is sufficient field evidence to substantiate the selection of such high au values for piles driven in soft clays, it is perhaps prudent to consider soil’s residual undrained strength in estimations of skin friction resistance, and conservatively ignore the gain in soil strength due to reconsolidation after pile driving. A discussion on challenges associated with predicting the skin friction resistance of piles with the α-Method is provided by Jardine et al. (2005) and a more rigorous method based on CPT measurements is presented in Section 6.12.7. The author recommends using the ICP method presented in Section 6.12.7 to, at least, evaluate predictions of skin friction resistance obtained with the α-method.

The end-bearing resistance Qb (units: force) is estimated by analogy to the conventional methods for calculating the collapse load of shallow foundations under undrained loading conditions:

(6.9) {Q_b} = {N_{cp}}{S_{u,b}}{A_b}

where Su,b is the undrained shear strength of the soil layer below the pile toe, Ab is the area of the pile base, and Ncp is the bearing capacity factor for undrained conditions which accounts for the shape of the failure surface developing below the pile toe, and is taken equal to {N_{cp}} = 9{\rm{ \:for \:}}{S_{u,b}} > 25{\rm{ kPa}} and {N_{cp}} = 6{\rm{ \:for \:}}{S_{u,b}} \le 25{\rm{ kPa}}.

Notice that the bearing capacity factor Ncp is higher than the bearing capacity factor Nc for a circular smooth or rough footing on undrained soil, discussed in Part 5. This accounts for the difference in the geometry of the failure surface that will develop below the pile’s toe, as discussed earlier. It is also worth noting that Qb of friction piles installed in clay is expected to be of the order of 20% of Qsf (Jardine et al. 2005).

License

Icon for the Creative Commons Attribution 4.0 International License

Fundamentals of foundation engineering and their applications Copyright © 2025 by University of Newcastle & G. Kouretzis is licensed under a Creative Commons Attribution 4.0 International License, except where otherwise noted.

Share This Book