5.5 Bearing capacity of footings on layered soils

George Kouretzis

5.5 Bearing capacity of footings on layered soils

5.5.1 Critical thickness of the surficial soil layer

One of the key assumptions of the common analytical solutions presented in Chapter 5.4 is that of uniform soil conditions, which is rarely the case in practice. When the geotechnical investigation reveals a non-uniform soil profile, we have to estimate whether the thickness of the top soil layer, measured below the embedment depth, is enough so that the failure surface will develop entirely inside it (Figure 5.36).

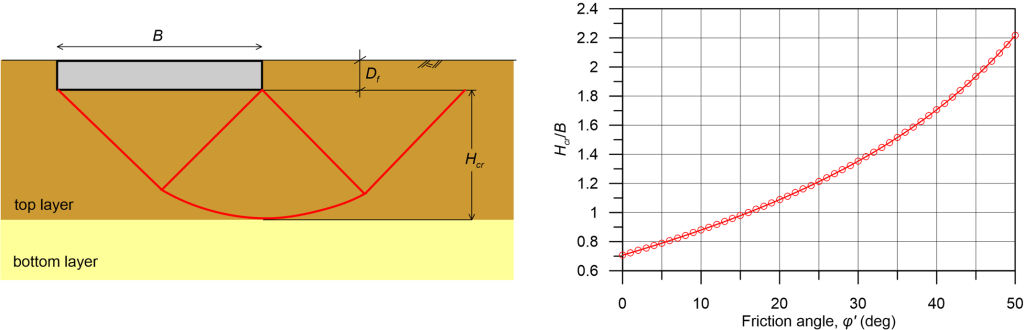
The figure on the left presents a footing of width B embedded in soil at depth Df. The top soil layer has thickness H_cr, measured from the elevation of the footing's base. Underneath the top soil layer there is a different bottom soil layer. A generalised failure mechanism develops underneath the footing inside the top layer, and the mechanism extends up to a depth H_cr, measured from the elevation of the footing's base. The figure on the right presents the variation of the parameter H_cr/B as function of the friction angle of the top soil layer. — Figure 5.36. Definition of the critical thickness, *H_cr* for failure to develop within the surficial soil layer.

It is reasonable to assume that if the thickness of the soil layer below the foundation, H_cr is less than the depth that the Prandtl mechanism penetrates into the soil (Figure 5.26) the failure surface will be entirely contained in the top soil layer, and the subsoil can be considered as homogeneous for bearing capacity calculations.

(5.35) 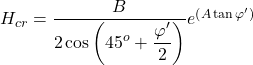${H_{cr}} = \dfrac{B}{{2\cos \left( {{{45}^o} + \dfrac{{\varphi '}}{2}} \right)}}{e^{\left( {A\tan \varphi '} \right)}}$

Where A = (45°+φ′/2) in rad.

Alternatively, the critical thickness H_cr can be calculated as (Budhu 2011):

(5.36) 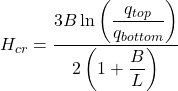${H_{cr}} = \dfrac{{3B\ln \left( {\dfrac{{{q_{top}}}}{{{q_{bottom}}}}} \right)}}{{2\left( {1 + \dfrac{B}{L}} \right)}}$

where:

q_topis the bearing capacity of the footing with the particular dimensions, resting on the surface of an infinitely deep layer with the properties of the top soil layer, and
q_bottom is the bearing capacity of the footing with the particular dimensions, resting on the surface of an infinitely deep layer with the properties of the bottom soil layer.

If the thickness of the top soil layer measured below the embedment depth, H_topis less than the critical thickness, H_cr, there is no general analytical method to estimate the bearing capacity, except of course numerical methods. Some characteristic cases are examined in the following paragraphs.

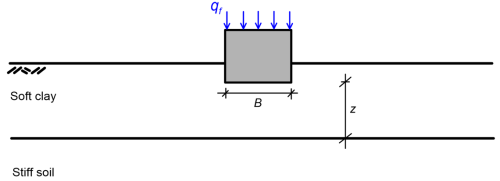
5.5.2 Footing on a soft clay layer overlying a stiff soil formation

In the case where a thin soft clay formation is found near the ground surface, good engineering practice suggests excavating the soft clay layer, and replacing it with well-compacted coarse-grained fill material. Founding structures directly on soft clays with shallow foundation should be avoided, except light structures such as one-storey buildings.

Experimental results have shown that in the case of a footing resting on soft clay overlying a stiffer stratum, the mechanism of bearing capacity consists of lateral squeezing of the soft soil, as the footing “sinks” into the top layer. Tomlinson and Boorman (1995) proposed the following expressions to estimate bearing capacity in that case:

Schematic of a footing embedded in a soft clay layer. The width of the footing is B. The footing is loaded with a pressure qf. The thickness of the soft clay layer is z, measured from the footing's base. Underneath the soft clay layer there is a stiff soil layer. — Figure 5.37. Footing on a soft clay layer overlying a stiff soil formation.

For circular/square footings:

(5.37) ${q_f} = \left( {\dfrac{B}{{2z}} + \pi + 1} \right){S_u}{\rm{ \:for \:}}\dfrac{B}{z} \ge 2$

For strip footings:

(5.38) ${q_f} = \left( {\dfrac{B}{{3z}} + \pi + 1} \right){S_u}{\rm{ \:for\: }}\dfrac{B}{z} \ge 6$

where z is defined in Figure 5.37 above. When B/z < 2 for circular/strip footings or B/z < 6 for strip footings (Figure 5.37), the expressions for homogeneous soil should be rather used.

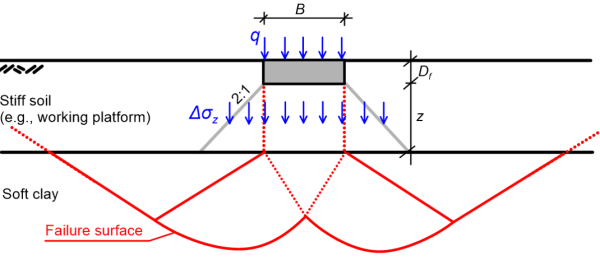
5.5.3 Footing on stiff soil overlying a soft clay layer

This case could well correspond to the common problem of a footing resting on a foundation improvement layer made of well-compacted coarse-grained fill, overlying a soft subgrade. A “punching” failure mechanism may develop under these circumstances (Figure 5.38a).

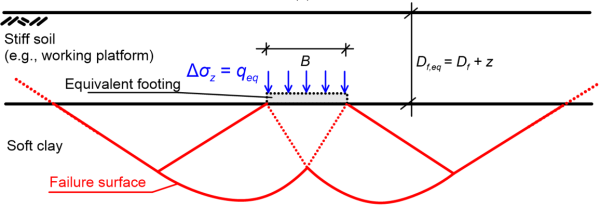
A simplified method for estimating the bearing capacity of a footing of any shape resting on the surface of, or embedded in a stiff soil formation overlying a soft clay layer consists of the following steps: First, we estimate the bearing capacity of the footing while considering uniform soil with the properties of the top stiff soil layer, which must not be critical for the design.

Accordingly, we estimate using Eq. 5.24 the net bearing capacity q_eq of a hypothetical equivalent footing with the same shape and dimensions, embedded at a depth D_f,_eq= D_f+z equal to the thickness of the top stiff soil layer (Figure 5.38). Bearing capacity failure of the actual footing will be reached when the vertical stress Δσ_z transferred from the actual footing to the interface of the stiff soil-soft clay layer (Figure 5.38b) becomes equal to q_eq i.e., Δσ_z = q_eq. The following approximate expressions can be used to calculate Δσ_z, while assuming 2:1 stress distribution (see Chapter 3.6):

For a rectangular footing:

(5.39) $\Delta {\sigma _z} = q\left[ {\dfrac{{BL}}{{\left( {B + z} \right)\left( {L + z} \right)}}} \right]$

For a square/circular footing:

(5.40) $\Delta {\sigma _z} = q{\left[ {\dfrac{B}{{\left( {B + z} \right)}}} \right]^2}$

For a strip footing:

(5.41) $\Delta {\sigma _z} = q\left[ {\dfrac{B}{{\left( {B + z} \right)}}} \right]$

in the above expressions q is the net bearing capacity of the actual footing. Therefore substituting Δσ_z= q_eq in the Eqs. 5.39 to 5.41 that corresponds to the actual footing shape will provide its net bearing capacity q. If the actual footing is embedded in soil, its bearing capacity will be q_f = q + γD_f.

Schematic of a footing embedded in stiff soil, at depth Df, underlaid by soft clay. The width of the footing is B. The footing is loaded with a pressure qf. The thickness of the stiff soil layer is z, measured from the footing's base. Vertical stresses from the footing are distributed with a 2:1 distribution, and a composite failure mechanism develops consisting of two shear bands in the stiff soil and a generalised failure surface in the soft clay. — Figure 5.38a. Punching of a footing into the underlying soft clay layer.

Schematic of an equivalent footing embedded in stiff soil, at depth Df,eq=Df+z, underlaid by soft clay. The width of the footing is B. The footing is loaded with a pressure qeq. The thickness of the stiff soil layer is Df+z, measured from the surface. A generalised failure mechanism develops in the soft clay. — Figure 5.38b. Concept for estimating the bearing capacity accounting for the development of the failure surface inside the soft clay layer.

Note that the methodology described above conservatively ignores the shear resistance of the top layer, and the energy dissipated along the shear planes located with it. Another simplifying assumption is that the inclination of the shear planes relative to the vertical in the top layer is ignored i.e., the width of the equivalent, hypothetical footing is taken equal to the width of the real one. There are more refined methods in the literature that do not require introducing these assumptions, however their range of application is limited to specific footing geometries and soil types. Such a method has been developed by Salimi Eshkevari et al. (2019a) for estimating the bearing capacity of strip footings resting on the surface of a sand layer overlying a soft clay, which is relevant to the design of working platforms for tracked plants. Salimi Eshkevari et al. analysed the results of a series of Finite Element Limit Analyses and concluded to the following expression that provides the bearing capacity of a strip footing on a layered profile of sand over clay q_f,_l:

(5.42) ${q_{f,l}}B = \gamma {H^2}{K_{sr}}\tan \varphi ' + {N_{cu}}{S_u}\left[ {B + 2H\tan \theta } \right] + \gamma {H^2}\tan \theta \le qB$

where B is the footing width, H is the thickness of the sand layer, γ is the unit weight of sand, φ′ is the friction angle of sand, S_u is the undrained shear strength of the clay layer, N_cu= 5.14 is the bearing capacity factor for strip footings on undrained soil, q is the bearing capacity of a footing of width B resting on the surface of uniform sand, calculated according to Eq. 5.25. The angle θ that provides the inclination of the shear planes that will develop in the sand layer can be calculated as:

(5.43) $\theta ({\rm{rad}}) = \alpha \ln \left( {\dfrac{{{S_u}}}{{\gamma H}}} \right) + \beta$

(5.44) $\alpha = 0.039\ln \left( {\tan \varphi '} \right) - 0.164$

(5.45) $\beta = 0.597\ln \left( {\tan \varphi '} \right) - 0.051$

Note that angle θ can be positive or negative. Thus, unlike the approximate method described above, the width B+2Htanθ of the equivalent footing in Figure 5.38 can be greater, or less than the width of the actual footing B. Finally, the punching shear coefficient K_sr, that is correlated with the normal stress acting on the shear planes that will develop in the sand layer, is calculated as:

(5.46) ${K_{sr}} = \delta \left( {\dfrac{{{S_u}}}{{\gamma H}}} \right) + 2$

(5.47) $\delta = - 3.45\left( {\tan \varphi '} \right) + 8.693$

5.5.4 Strip footings on layered sands

Estimation of the bearing capacity of strip footings resting on the surface of a relatively thin layer of dense sand overlaying a weak layer of loose sand underpins the design of working platforms for heavily loaded tracked piling rigs and cranes, on sites which loose sand deposits are found at the ground surface. Hanna (1981) was among the first to study this problem, and concluded to the following expression for estimating the bearing capacity in terms of stress when a punching failure mechanism develops:

(5.48) ${q_{f,l}} = {q_b} + \gamma {H^2}\dfrac{{{K_s}\tan {{\varphi '}_1}}}{B} - {\gamma _1}H \le q$

where B is the footing width, H is the thickness of the top (dense) sand layer, γ₁ is the unit weight of the dense sand layer, φ′₁ is the friction angle of the dense sand layer, q_b is the bearing capacity of a footing of width B embedded at depth H in a uniform sand layer with the properties of the loose sand, calculated as:

(5.49) ${q_b} = 0.5{\gamma _2}B{N_{\gamma 2}} + {\gamma _1}H{N_{q2}}$

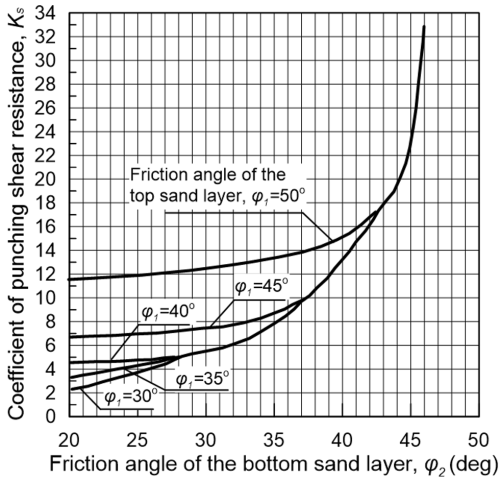
where γ₂ is the unit weight of the loose sand layer, while Ν_γ₂ and Ν_q2 are the bearing capacity factors of the loose sand layer, featuring friction angle φ′₂, calculated according to Eq. 5.18 and Figure 5.31, respectively. Moreover, q in Eq. 5.48 is the bearing capacity of a footing of width B resting on the surface of uniform dense sand with friction angle φ′₁ , calculated according to Eq. 5.25, and K_s is a punching shear resistance coefficient that depends on the friction angles of the two sand layers, and is provided in Figure 5.39.

Graph showing the variation of the coefficient of punching shear resistance K_s, with the friction angle of the bottom sand layer φ2. Different curves corresponds to different friction angles of the top sand layer φ1, ranging from 30 deg to 50 deg. — Figure 5.39. Determination of the coefficient of punching shear resistance *K_s* for strip footings on layered sand (after Hanna 1981).

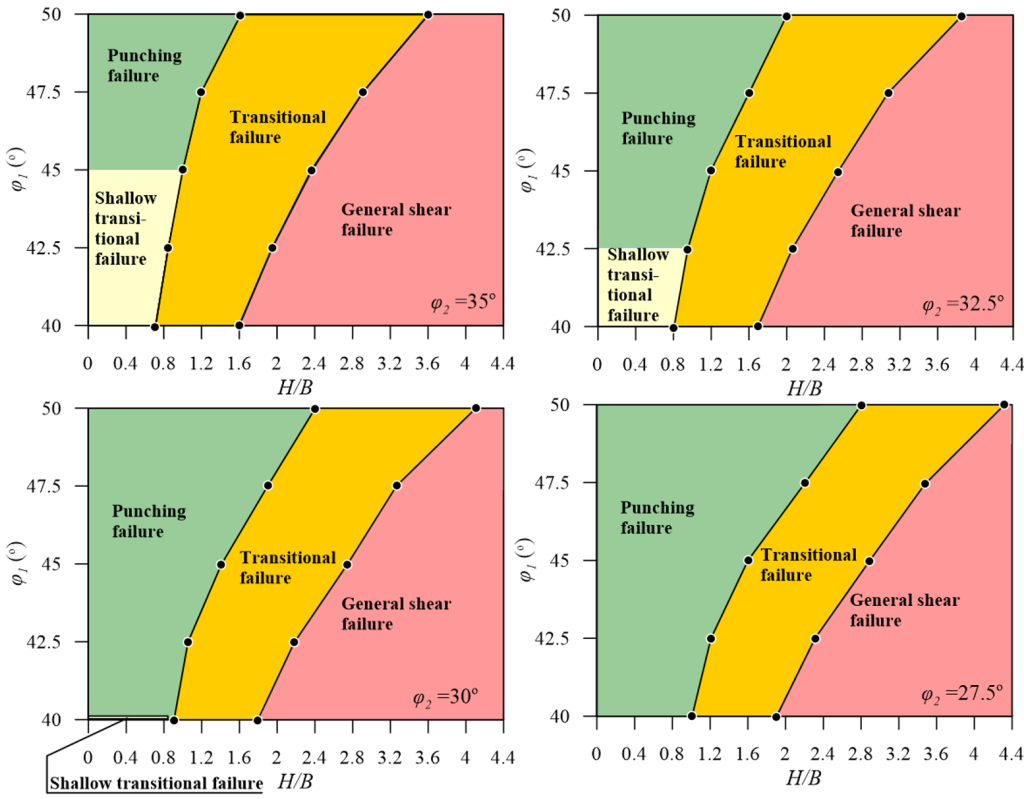
Four graphs depicting zones corresponding to different failure modes (punching, transitional, general shear and shallow transitional failure) depending on the combination of friction angle φ1 and the parameter H/B. Each one of the graphs corresponds to a different value of the friction angle φ2. — Figure 5.40. Failure mechanisms for strip footings on layered sand for different friction angles and dimensionless thickness *H/B* combinations (Salimi Eshkevari et al. 2019b).

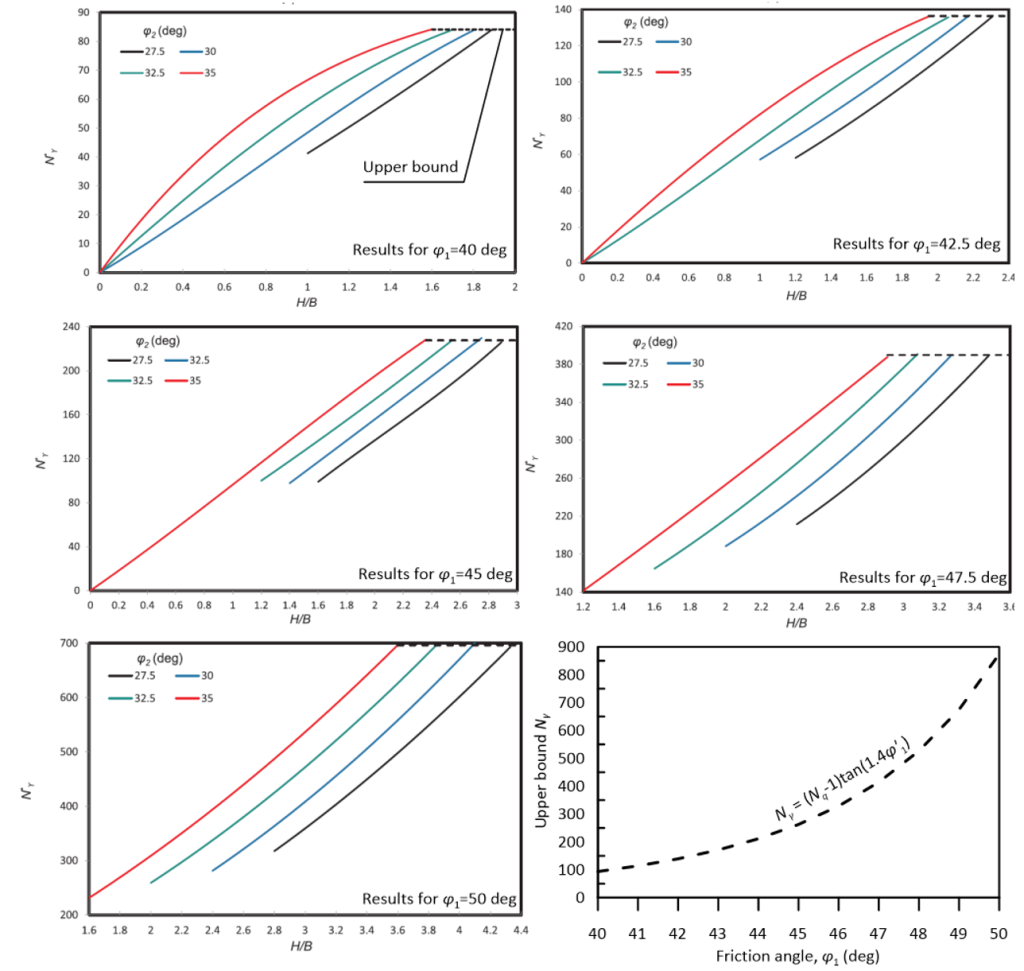
An important assumption underlying Hanna’s Eq. 5.48 is that a punching failure mechanism develops, irrespective of the relative strength of the two layers. Salimi Eshkevari et al. (2019b) have shown that the failure mechanism that will develop depends on the friction angles of the two layers, as well as the ratio of the thickness of the top dense sand layer over the width of the footing H/B. Using Figure 5.40 one can determine which failure mechanism will develop. Accordingly, Salimi Eshkevari et al. (2019b) proposed the following expression for calculating the bearing capacity of a strip footing resting on dense sand over loose sand, for the cases where a transitional (or shallow transitional) mechanism is expected to develop:

(5.50) ${q_{f,l}} = 0.5{\gamma _1}BN_\gamma ^ * \le q$

where the modified bearing capacity factor N_γ* is given in Figure 5.41 for different values of φ′₁, φ′₂ and H/B. If Figure 5.40 suggests that a punching failure mechanism will develop, Salimi Eshkevari et al. recommended using Hanna’s expression (Eq. 5.48) to determine the bearing capacity. Bearing capacity factor values in Figure 5.41 are applicable to the case where γ₁/γ₂ = 1.2, which is probably a reasonable approximation for most practical cases. Note also that Figure 5.41 covers only specific H/B ranges for which a transitional mechanism will develop. Finally, the upper bound to the bearing capacity factor N_γ* (dashed lines in Figure 5.41) is the conventional bearing capacity factor Ν_γ, and indicates cases where the thickness of the top dense sand layer exceeds the critical thickness, thus a general shear failure mechanism will develop and q_f,_l = q.

Five graphs presenting the variation of the factor N*γ as function of the parameter H/B. Each one of the graphs corresponds to a different value of the friction angle φ1. Each graph contains multiple curves, with each curve corresponding to a different φ2 value. The upper bound of the factor N*γ is indicated in each graph with a dashed line. The figure on the bottom right presents the value of the upper bound Nγ as function of the friction angle φ1. The expression that provides the upper bound is Nγ=(Νq-1)tan(1.4φ1') — Figure 5.41. Modified bearing capacity factor N_γ* for different values of *φ′₁*, *φ′₂* and *Η/Β* (Salimi Eshkevari et al. 2019b) and upper bound bearing capacity factor *N_γ* for generalised failure according to Meyerhoff.

5.5.5 Footings on multi-layered soil profile

A lower-bound estimate of the bearing capacity of a footing resting on a multi-layered soil profile can be found by simply considering a homogeneous soil with the properties of the weakest layer, an approach that may lead to perhaps over-conservative results. Numerical methods are recommended for the treatment of such problems.

License

Icon for the Creative Commons Attribution 4.0 International License

Fundamentals of foundation engineering and their applications Copyright © 2025 by University of Newcastle & G. Kouretzis is licensed under a Creative Commons Attribution 4.0 International License, except where otherwise noted.