"

4.8 Evolution of primary consolidation settlement with time

The rate of dissipation of excess pore water pressure, and thus the necessary time for the applied loading on the ground surface to be transferred to the soil skeleton resulting in increase of the effective stress, depends on the permeability, k of the soil. We can obtain a closed-form analytical expression that provides the rate of dissipation of excess pore pressure, and thus the evolution of settlement with time (Figure 4.7), under some simple assumptions:

  • 1-D conditions prevail, with water flowing only vertically, as in the oedometer test (Figure 4.27).
  • The soil is fully saturated, homogeneous and isotropic.
  • Darcy’s law is valid, thus flow q is equal to the permeability times the hydraulic gradient i i.e., q=ki
  • Small strains.

Under the above assumptions, Terzaghi formulated the one-dimensional consolidation equation, describing the variation of excess pore pressure u with time t and depth z as:

(4.65) \dfrac{{\partial u}}{{\partial t}} = {c_v}\dfrac{{{\partial ^2}u}}{{\partial {z^2}}}

The constant cv in the differential equation 4.65 is called coefficient of consolidation, and depends on the coefficient of volume compressibility mv and the soil permeability in the vertical direction kz as:

(4.66) {c_v} = \dfrac{{{k_z}}}{{{m_v}{\gamma _w}}}

where γw ≈ 10 kN/m3 is the unit weight of the water. The coefficient of consolidation carries units of length2/time.

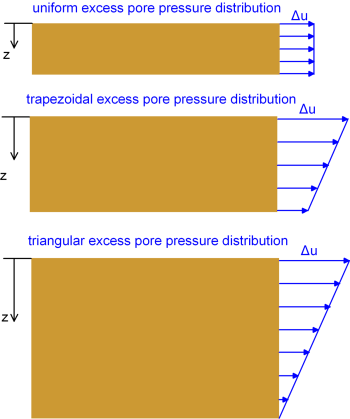
Solution of the differential equation 4.65 requires knowing the initial distribution of excess pore pressure with depth (Figure 4.38), and the permeability boundary conditions. For example, assuming uniform excess pore pressure distribution with depth, corresponding to a relatively thin clay layer (Figure 4.38) and double drainage, both from the top and the bottom of the layer (Figure 4.39a):

  • at t = 0, the excess pore pressure will be uniform along the thickness, and equal to the applied pressure at the surface Δu0 = qext
  • at the top boundary z=0 where drainage is allowed, Δu = 0
  • at the bottom boundary z=H where drainage is allowed too, Δu = 0
Illustration of three initial excess pore pressure Δ_u distributions: uniform, trapezoidal, and triangular. The uniform pore pressure distribution is applicable to the thinner soil layer, and the triangular pore pressure distribution to the thicker soil layer.
Figure 4.38. Initial excess pore pressure distribution with depth, for increasing thickness of the compressible layer.

The drainage boundary conditions suggest that excess pore pressure will immediately fall to zero at the permeable boundaries.

A closed-form solution of Eq. 4.65 exists for the above conditions and provides the variation of the excess pore pressure with depth at different time instances (Figure 4.40):

(4.67) \Delta u\left( {z,t} \right) = \sum\limits_{m = 0}^\infty {\dfrac{{2\Delta {u_0}}}{M}\sin \left( {\dfrac{{Mz}}{{{H_{dr}}}}} \right)} {e^{ - {M^2}{T_v}}}

where M = \dfrac{{\pi \left( {2m + 1} \right)}}{2}, and Tv is the time factor, equal to:

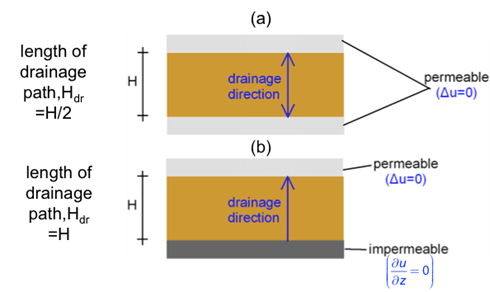
The figure on the top presents the flow boundary conditions for a soil specimen where drainage is allowed from both the top and bottom of the sample. The excess pore pressure at the top and bottom of the sample are Δu=0 and the length of the drainage path is half the thickness of the sample. The figure on the bottom presents the flow boundary conditions for a soil specimen where drainage is allowed only from the top of the sample. The excess pore pressure at the top is Δu=0, and the gradient of the excess pore pressure at the bottom is zero. The length of the drainage path is equal to the thickness of the sample.
Figure 4.39. Boundary conditions and length of drainage path for (a) double drainage, and (b) drainage only from the top of the soil layer.

(4.68) {T_v} = \dfrac{{{c_v}t}}{{H_{dr}^2}}

The length of the drainage path, Hdr depends on the drainage boundary conditions, and is depicted in Figure 4.40.

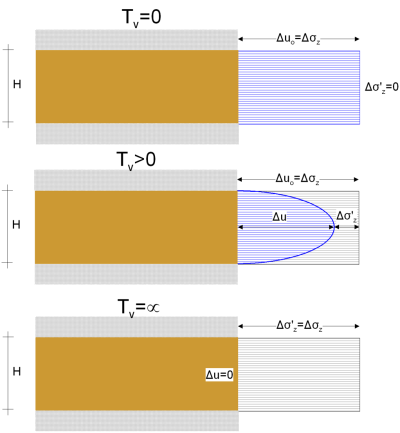
Graph depicting the distribution of excess pore pressures along a sample of thickness H where drainage is allowed from the top and bottom, at three different time instances defined via the time factor Tv. When Tv = 0 (top figure) the excess pore pressure is uniform across the sample, and equal to the applied stress. When Tv > 0 (mid figure) the excess pore pressure is zero at the top and bottom of the sample, and increases parabolically to its middle, where it attains its maximum value. When Tv is infinite (bottom figure) the excess pore pressure is zero across the entire sample.
Figure 4.40. Graphical representation of excess pore pressure distribution with depth at different time instances, calculated from Eq. 4.67.

Instead of using the absolute value the of excess pore water pressure, consolidation progress can be described via the degree of consolidation (or consolidation ratio), U(z) which defines the amount of consolidation completed at a particular time instance, at a specific depth, z:

(4.69) U\left( z \right) = 1 - \dfrac{{\Delta {u_z}}}{{\Delta {u_0}}}

The degree of consolidation is visualised as the grey shaded area in Figure 4.40. From an engineering point of view, we are rather interested in the average degree of consolidation, U of the whole compressible layer. For the special case where the initial excess pore pressure distribution is assumed constant with depth (Figure 4.38) the average degree of consolidation is calculated as:

(4.70) U = 1 - \sum\limits_{m = 0}^\infty {\dfrac{2}{{{M^2}}}} {e^{ - {M^2}{T_v}}}

The variation of the average degree of consolidation with the time factor Tv is illustrated in Figure 4.41.

Eq. 4.70 and Figure 4.41 are also valid when drainage is not allowed at the bottom of the clay layer. The length of the drainage path in that case will be Hdr = H (Figure 4.39). Note that at an impermeable boundary, the gradient of pore pressure will be zero \partial u/\partial z = 0.

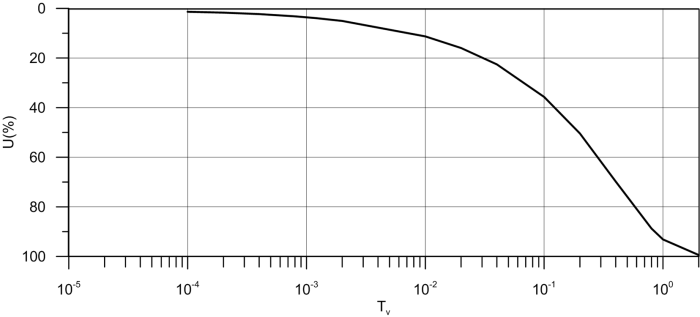
Graph depicting the variation of the average degree of consolidation U(%) with the time factor T_v,. When the time factor becomes Tv=1 the average degree of consolidation is about 90%.
Figure 4.41. Variation of the average degree of consolidation U with the time factor Tv for uniform initial excess pore water pressure distribution.

Note that Figure 4.41 can be used to estimate settlement of a 1-D soil column at any given time t1. By substituting t1 into the expression for the time factor Tv (Eq. 4.68) we can find the average degree of consolidation U1 at t1 directly from Figure 4.41. Therefore, settlement at t1 will be:

(4.71) {\rho _1} = \dfrac{{{U_1}\left( \% \right)}}{{100}}{\rho _{pc}}

where the primary consolidation settlement ρpc is calculated according to Section 4.6.2, assuming linear elastic or non-linear soil behaviour.

License

Icon for the Creative Commons Attribution 4.0 International License

Fundamentals of foundation engineering and their applications Copyright © 2025 by University of Newcastle & G. Kouretzis is licensed under a Creative Commons Attribution 4.0 International License, except where otherwise noted.

Share This Book