Chapter 3 – Present and Future Values with Applications
Chapter Learning Objectives
After completing this chapter, students should be able to
- Calculate the present value and future value for multiple cash flows
- Describe how to calculate the present value and future value of an ordinary annuity and annuity due
- Explain what (growing) perpetuities are and calculate the present values of (growing) perpetuities
3.1 Mixed cash flow stream
3.1.1 Future value of cash flow streams
Financial managers frequently need to evaluate series of cash flows that occur in future period. From the last chapter, the future value (FV) of a series of cash flows cannot be found by simply summing them up. Each individual cash flow needs to be converted to a common point in time in the future and then sum up. The following example illustrates this principle:
Mary wants to determine the balance in an investment account earning 9% annual interest. She makes the following ends of year deposits as follows: $500 in year 1, $900 in year 2, $400 in year 3, $700 in year 4.
Where i = 9%:
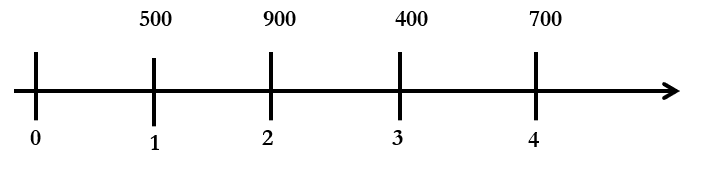
The future value of this stream of cash flow can be found by bringing the value of each of the cash flow to year 4.
FV = 500×(1+0.09)3 + 900×(1+0.09)2 + 400×(1+0.09)1 + 700
= 647.51 + 1069.29 + 436 +700
= $2,852.8
3.1.2 Present value of multiple cash flows
Just as with future value, the present value (PV) of multiple cash flows is determined by summing up the present values of each individual cash flow. Each cash flow is discounted back to the current period to reflect its value in today's terms.
For example, if you expect to receive $100 in one year, $200 in two years, and $300 in three years, and the discount rate is 5%, you would discount each of these cash flows back to their present value. The sum of these present values would give you the total current worth of your future cash flows.
Where i = 5%
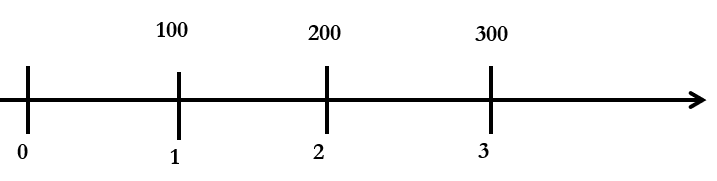
PV = 300/(1+0.05)3 + 200/(1+0.05)2 + 100/(1+0.05)
= 285.71 + 181.41 + 95.24
=$562.36
3.2 Annuity: A special case of level cash flows
An annuity is a stream of equal periodic cash flows over a stated period of time. This stream of cash flows can represent regular inflows from an investment or outflows as committed expenses that need to occur in the future. Annuities are often associated with retirement income, however, their application is not limited to retirement income. Rather mortgage payments, insurance premium, rent and lease payments can all be classified as annuities.
For a stream of cash flows to be qualified as an annuity, it needs to meet three conditions:
- The amount of cash flows are the same each period.
- The interval between each cash flow is the same.
- The cash flows occur for a fixed amount of time i.e. they do not go on forever.
There are two types of annuity:
Ordinary annuity: is an annuity where cash flows are received and paid at the end of each period. Example: mortgage repayments, salaries, insurance premiums.
Annuity due: is an annuity where cash flows are received and paid at the beginning of each period. Example: tuition payment, rent.
3.2.1 The future value of an ordinary annuity
The future value of an ordinary annuity refers to the amount of money that will be accumulated in the future when a series of equal payments are made at the end of consecutive periods at a certain interest rate.
Here is the timeline of the cashflows for an ordinary annuity:
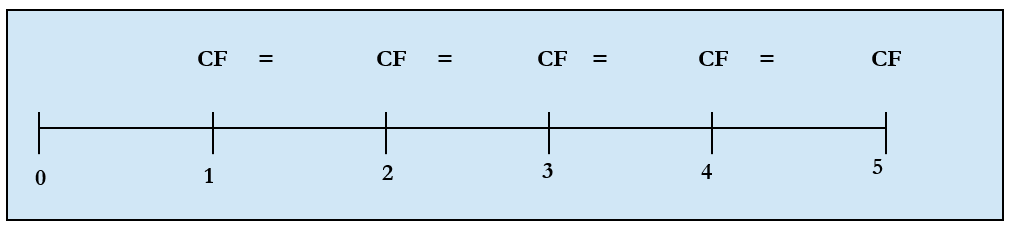
To calculate the future value of an ordinary annuity, one option is to bring each of the cash flow to the future i.e. end of period 5 and add them up just like any other stream of cash flow. However, there is a quicker way. The future value of an ordinary annuity can be computed according to the following formula:
Equation 1:
[latex]FVA=\frac{CF}{i}\times\left[\left(1+i\right)^n-1\right][/latex]
[latex]={CF}\times\frac{{({1}+{i})}^{n}-{1}}{{i}}[/latex]
[latex]={CF}\times\frac{{Future}\ {value}\ {factor}\ -{1}}{{i}}[/latex]
Where:
- FVA: future value of an annuity,
- i: interest rate per period,
- CF: cash flow each period and
- n: number of the periods.
Example: Suppose you are saving for retirement and decide to deposit $1,000 into your retirement fund at the end of each year for the next 20 years. Assume the retirement fund offers an annual interest rate of 5%. At the end of year 20, what is the balance of your retirement account?
Since the deposits are made at the end of each year over a span of 20 years, this pattern of payment qualifies as an ordinary annuity and the formula in Equation 1 can be applied to calculate the accumulate amount at the end of the 20th year. The example also shows that when cash flows happen for a long period of time, bring each cash flow to the future is very time consuming and hence not realistic. Equation 1 offers a far better alternative.
Answer: N = 20, i = 5% and CF = 1000.
Future value factor is (1 + 0.05)20 -1 = 1.6533
FV = 1000 * 1.6533/0.05 = $33,066
3.2.2 The future value of an annuity due
For annuity due, the cash flow pattern is very similar to the ordinary annuity. The only difference is each payment occurs at the beginning of the period rather than in the end. The timeline of the cashflows for an annuity due is as follows:
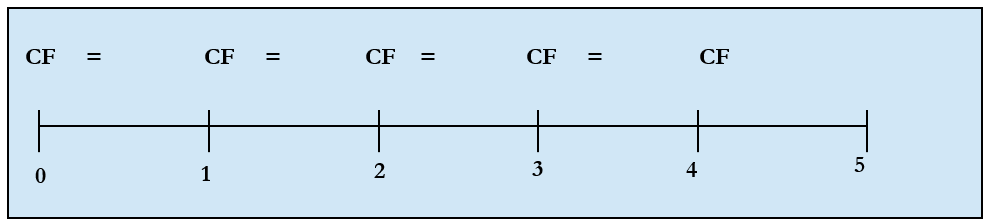
In an annuity due, each payment accrues interest for an additional period compared to an ordinary annuity, because payments in an annuity due are made at the beginning rather than at the end of each period. Consequently, the future value of an annuity due will always exceed the future value of an ordinary annuity when both have identical cash flows and the same duration.
The future value of an annuity due is therefore:
Equation 2:
[latex]FV=FV of Ordinary Annuity ×\left(1+i\right)[/latex]
[latex]=CF\times\frac{{(1+i)}^n-1}{i}\times(1+i)[/latex]
Example: Suppose you are saving for retirement and decide to deposit $1,000 into your retirement fund at the beginning of each year for the next 20 years. Assume the retirement fund offers an annual interest rate of 5%. At the end of year 20, what is the balance of your retirement account?
Answer: The only difference between this example and the above example is the deposit is made at the beginning of each period instead of the end. This stream of cashflow is therefore classified as an annuity due and the future value can be calculated as:
Future value of an annuity due = Future value of an annuity * (1 + i)
= 33,066 * (1+0.05) = $34,719.3
3.2.3 Present value of an ordinary annuity
The present value of an ordinary annuity measures the current worth of a series of future periodic payments at a given interest rate. It answers the question: "How much would I have to invest today to receive a certain payment amount at regular intervals for a specified period, given a particular interest rate?"
The formula for the present value of an ordinary annuity is given by:
Equation 3:
[latex]PV=PVA=\frac{CF}{i}\times\left[1-\frac{1}{{(1+i)}^n}\right][/latex]
[latex]=CF\times\frac{1-1/{(1+i)}^n}{i}[/latex]
[latex]=CF\times\frac{1-Present\ value\ factor}{i}[/latex]
Example: If you require $5,000 every month to live for the next 20 years starting by next month. How much money should you deposit into your account now if the bank is paying an interest of 6% p.a?
Answer: The sum you need upfront is essentially the present value of an ordinary annuity, with each payment being $5,000. Since the payments are monthly over 20 years, you have a total of 240 payment periods (12 months x 20 years). The monthly interest rate is 0.5% (which is the annual rate of 6% divided by 12 months).
Applying the formula in equation 3, CF = $5,000, (1 + 0.005)240 is 0.3021. PV = 5000 (1 – 0.3021)/0.005 =$697,903.86.
In order to receive $5,000 per month starting from the next month, you need to deposit $697,903 today if the bank is paying an interest of 6% p.a.
3.2.4 Present value of an annuity due
Just as with the future value, the present value of an annuity due is obtained by adjusting the present value of an ordinary annuity forward by one additional period.
The formula for the present value of an annuity due can be given by:
Equation 4:
[latex]PV=PV\ of\ ordinary\ annuity\times(1+i)[/latex]
[latex]=\frac{CF}{i}\times\left[1-\frac{1}{{(1+i)}^n}\right]\times(1+i)[/latex]
Example: Suppose you still require $5000 monthly payment to fund your lifestyle expenses for the next 20 years with the first payment needed immediately. How much you need to deposit now if the bank is paying an interest of 6% p.a?
Answer: Since the first payment is required immediately, this stream of cashflow is classified as an annuity due. The first payment happens at month 0 while the last payment happens at month 19. The present value of an annuity due can be obtained by compounding the present value of an ordinary annuity one more period.
PV of an annuity due = PV of an ordinary annuity * (1 + i)
= 697,903 * (1+0.005) = $701,595.38.
Similar to future value, the present value of an annuity due is always higher than the present value of an ordinary annuity.
3.2.5 Application of an annuity formula
The application of an annuity extends beyond calculating present and future value. The formula allows investors to establish monthly payment amounts, discern the growth or discount rate necessary to reach a specified future sum, or determine the duration required for an investment to mature to a desired lump sum. The annuity equation comprises four variables; by knowing any three, the remaining one can be deduced by rearranging the equation.
Example: You need $200,000 as a deposit to buy your new home. If the interest rate is 6% p.a and you can only put aside maximum $3,500 per month towards this saving goal. How long will it take you to achieve your initial deposit for your home? Assume the first payment will start 1 month from now.
Answer: $200,000 is the Future Value that your monthly payments will grow to. Interest per period is 0.06/12 = 0.005 or 0.5% per month since each payment is made monthly, what you need is monthly interest rate. $3500 is the amount that you need to pay every month in order to achieve a future lumpsum of $200,000. Since the first payment commences one month from now, it is an ordinary annuity. What we need to find is the number of periods that required to reach $200,000
Applying the formula in equation 1:
[latex]{FVA}=\frac{{CF}}{{i}}\times\left[{({1}+{i})}^{n}-{1}\right][/latex]
[latex]200000=\frac{3500}{0.005}\left[\left(1+0.005\right)^n-1\right][/latex]
[latex]200000=700000\left[\left(1+0.005\right)^n-1\right][/latex]
[latex]\left[\left(1+0.005\right)^n-1\right]=200000/700000[/latex]
[latex]\left[\left(1+0.005\right)^n-1\right]=0.2857[/latex]
[latex]\left(1+0.005\right)^n=0.2857+1[/latex]
[latex]1.005n = 1.2857[/latex]
In order to solve for n, we take log on both sides, n*log(1.005) = log(1.2857), n=log(1.2857)/log(1.005). N = 50.39 periods and since each period is 1 month, if each month you put aside $3500 and the bank is paying an interest of 6% per annum, you need to save 50.39 moths or 4.2 years to reach $200,000.
3.3 Perpetuities
3.3.1 Present value of a perpetuity
A perpetuity is defined as a stream of equal cash flows that continue indefinitely. It's a type of annuity that has no end, theoretically lasting forever. For instance, dividend distributions can be regarded as a form of perpetuity since the company is assumed to operate on a going concern basis. Although companies might not exist forever, in the perspective of investors, the lifespan of a company is considered to be indefinite.
A perpetuity does not have a future value since its life is indefinite. The present value of a perpetuity is given by:
Equation 5:
[latex]PV=\frac{CF}{i}[/latex]
Example: Your grandfather is retiring at the end of next year. He would like to ensure that he and after he dies his heirs, will receive payments of $11,309 a year forever, starting when he retires. If he can invest at 9.9% per annum, how much does your grandfather need to invest NOW to receive the desired cash flow?
Answer: The amount of money he needs to invest now is the present value of the perpetuity where each cashflow is $11,309, interest rate is 9,9% or 0.099.
[latex]PV=\frac{CF}{i}[/latex]=[latex]\frac{11,309}{0.099}=$114,232.32[/latex]
3.3.2 Growing Perpetuities
A growing perpetuity is a series of cash flows that increase at a constant rate indefinitely. Unlike a standard perpetuity, which has a fixed cash flow, a growing perpetuity takes into account the growth of the payments over time.
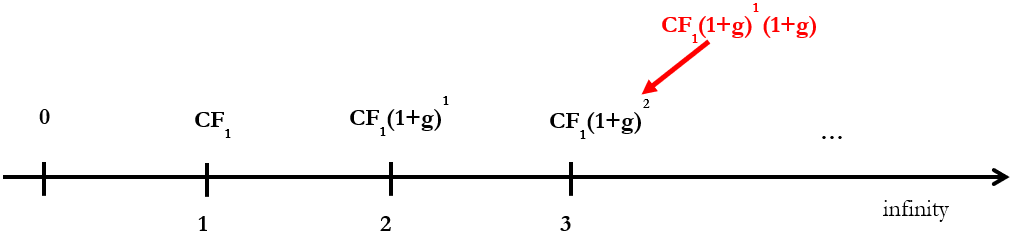
The CF1 grows at a constant rate (g) year on year forever.
Equation 6:
[latex]PV\ of\ a\ growing\ perpetuity=\frac{{CF}_1}{i-g}[/latex]
Example: As a millionaire intending to establish a scholarship in your name, you wish to grant an annual scholarship of $50,000, with the amount increasing by the inflation rate of approximately 3% each year. If the interest rate is 7% p.a, how much do you need to put down today to ensure the scholarship can be sustained indefinitely?
Answer: This is a growing perpetuity since the payment required in the first year is $50,000. In the second year, the required repayment is 50,000 * (1 + 0.03) = $51,500. In the third year, the payment would be 51,500 * 1.03 and so on. The amount that you need to put down today would be the present value of this growing perpetuity where the growth rate is 3% p.a and interest rate is 7% p.a.
[latex]PV=\frac{{CF}_1}{i-g}[/latex] = [latex]\frac{50,000}{0.07-0.03}=$1,250000[/latex]
Takeaways and looking ahead
This chapter wraps up our discussion on the present and future values of single and multiple cash flows. The forthcoming chapter will expand these valuation principles by applying the present and future value formulas to the valuation of more complex financial instruments, namely stocks and bonds. We will examine how these formulas assist investors in making informed decisions about the intrinsic value of these securities, taking into account expected future cash flows and risks.
References:
Graham, J., Smart, S. B., Adam, C., Gunasingham, B. Introduction to Corporate Finance (2nd Asia – Pacific Edition) 2017.
Brealey, R., Myers S. C., Allen F., Edmans, A. Principles of Corporate Finance (14th Edition) 2022.
Peirson, G., Brown, R., Easton, S., Howard, P., Pinder, S. Business Finance (12th Edition) 2015.

