Chapter 2 – Present and Future Values
Chapter Learning Objectives
After completing this chapter, students should be able to
- Define and discuss the principle time value of money.
- Define and contrast future and present values.
- Able to move cashflows from the present to the future and vice versa
- Distinguish between compounding versus discounting
- Understand the concept of discount rate.
1. Basic Principles of Finance
In finance, we focus on cashflows, not accounting profit. There are two types of cashflows: cash receipts are denoted as cash inflows while cash payments are denoted as cash outflows. When assessing investment opportunities, financial managers are not only concerned with the magnitude of the cashflows but also the timing and risks of these expected cashflows. The overarching principle that influences how managers value future cashflows and hence what investment decisions to make is the time value of money which states that “A dollar received today is always worth more than a dollar received in the future”.
1.1 Why is a dollar today always worth more than a dollar in the future?
The reason is money available today can be invested and grow. When someone invests, they expect to be compensated in some form of “returns” but how large should these returns be? There are three components that make up the rate of returns.
First, by investing, the investor is deferring consumption today in anticipation of consuming more in the future. That is, the investment has to grow in real terms in order for the investor to consume more. Second, when an individual’s money is tied up in investments, the value of that money can be eroded by inflation. Thus, the rate of return has to be high enough to also cover the inflation rate. Finally, there may be risks associated with the investment. The future returns on an investment are not guaranteed and there is a possibility of not receiving the expected return, or in worse case scenarios, losing the initial capital. Investments that carry higher risks typically need to offer higher returns to attract investors. Taken together, the invested funds should yield a return that compensates for the delay in consumption, inflation and risk.
Total Return = Inflation rate + Real interest rate + Risk premium
1.2 What about interest rate? Is it a form of return?
Interest refers to the return on debt investment, where the investor lends money to an entity (such as a corporation, government, or financial institution) in exchange for the promise of future repayments. Interest rate is often expressed as a % per annum (p.a).
Example: Suppose you invest $100 in a bank account that pays interest of r = 6% a year. In the first year, what is the interest that you earn and what is the value of your investment?
Answer: In the first year, the interest that you earn will be 0.06 * $100 = $6. The value of your investment will grow to $100 + $6 = $106 or $100 * (1+0.06) = $106.
2. Present and Future Values
2.1 Terminology
Before we proceed, let’s introduce some terminology:
- Nominal interest: is the stated interest rate on a financial product or investment e.g. 5% p.a.
- Principal refers to the amount of borrowing or lending.
- Time to maturity: is the duration from the current date until the date when the principal amount of a debt instrument is due to be repaid in full.
- Present value (PV) is the current worth of a future sum of money or stream of cash flows given a specific discount rate.
- Future value (FV) is the value of a current asset at a specified date in the future, based on an assumed rate of return over time.
- A discount rate refers to the rate of return used to discount future amounts of money, converting them into their equivalent present value.
2.2 Why is it necessary to distinguish between present and future values?
The distinction is crucial because these concepts serve unique purposes in financial decision-making. Present value helps in understanding the current worth of money that will be received or paid in the future which is vital for comparing the value of cash flows occurring at different times. Conversely, future value is used to determine how much a current sum of money will grow overtime. This assists in forecasting the growth of current investments which is crucial for long-term planning and setting realistic financial goals. Both concepts are grounded in the time value of money principle.
Example: Let's say you decide to deposit $100 into an account offering a 5% p.a. After one year, your investment grows to $100 multiplied by (1 + 0.05), which equals $105. Hence, the amount of $105 represents the future value of your $100 investment over a year, at a 5% annual interest rate.
Conversely, the $100 can be considered as the present value of $105, discounted back one year at a 5% annual rate. As an investor, if you know that the interest rate is 5% p.a then you are indifferent between receiving $100 now or $105 one year from now.
The process of going from the present value to the future value is called compounding, whereas the method of translating future amounts back to the present is referred to as discounting.
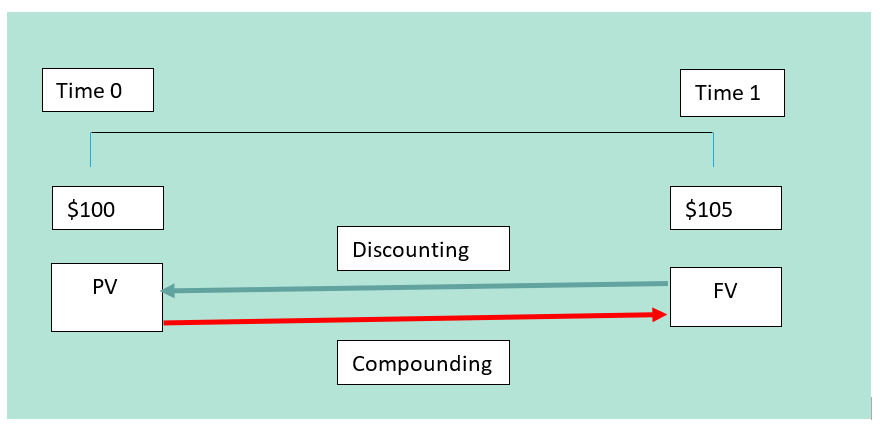
2.3. Present and Future Values
2.3.1 Calculating present and future value
The methods used to determine present and future values vary based on the kind of interest rate arrangement in place. Broadly speaking, there are two types of interest rate arrangements: simple interest and compound interest.
Simple interest is a method of accruing interest where the interest charge is calculated solely on the principal amount. Interest does not compound, interest earned is not reinvested to earn additional interest. The principal amount remains unchanged throughout the term of the loan or investment. Simple interest is often used in short-term borrowing and lending where the horizon is less than 1 year.
Compound interest is the method by which interest earned on a principal amount is reinvested, so that in subsequent periods, interest is then earned on the new principal, which includes the previously earned interest. This compounding effect leads to the principal amount growing over time, allowing the investor to earn “interest on interest”.
Example: What is the future value of $100 at the end of year 1 with interest rate of 6%?
Interest earned during the year will be $100 * 0.06 = $6. The future value or value at year 1 will be FV1 = $100 + $100 * 0.06 = $106. In this case, both simple and compound interest yield the same results.
Principal = PV = 100
r = 0.06 p.a.
n = 1
FV1 = 100 * (1 + 0.06) = 106
What is the future value of $100 at the end of year 2?
For compound interest, the interest will be calculated on the $106 balance. The interest earned during year 2 will be 0.06 * $106 = $6.36. Hence the future value or value at year 2 will be FV2 = $106 + $106 * 0.06 =112.36.
For simple interest, the interest will be calculated on the initial principal which does not change over time. So, the interest earned during year 2 is still 0.06 * $100 = $6. The future value or value at year 2 will be $106 + $100 * 0.06 = $112.
| Principal = PV = 100
r = 0.06 p.a. n = 2 Compound interest FV2 = FV1 * (1 + 0.06) = 100 * (1 + 0.06) * (1 + 0.06) =100 * (1 + 0.06)2 =112.36 |
Principal = PV = 100
r = 0.06 p.a. n = 2 Simple interest FV2 = FV1 + 100 * 0.06 = 100 + 100 * 0.06 +100 * 0.06 =100 * (1 + 0.06 * 2) =112 |
The difference of $0.36 is due to interest on interest under the compounding interest arrangement.
What is the future value of $100 at the end of year 5?
| Year | Compound interest | Simple interest |
| 1 | 100.00 * (1+0.06) = 106.00 | 100.00 * (1+0.06) = 106.00 |
| 2 | 106.00 * (1+0.06) = 112.36 | 100.00 * (1+0.06) + 6 = 112.00 |
| 3 | 112.36 * (1+0.06) = 119.10 | 100.00 * (1+0.06) + 12 = 118.00 |
| 4 | 119.10 * (1+0.06) = 126.25 | 100.00 * (1+0.06) + 18 = 124.00 |
| 5 | 126.25 * (1+0.06) = 133.82 | 100.00 * (1+0.06) + 24 = 130.00 |
| FV = PV (1+i)n = 100 * (1.06)5 = 133.82 | FV = PV * (1+ i * t)
= 100 * (1+0.06*5) = 130.00 |
As the investment horizon increases, the difference in future values between compound and simple interest arrangements becomes wider. This is because compound interest earns interest on the interest already earned, while simple interest only earns interest on the principal amount.
Future value formula for compound and simple interest:
Equation 1:
[latex]{\rm FV}_{compound}=PV×\left(1+i\right)^n[/latex]
Equation 2:
[latex]{FV}_{simple}=\ PV\times\left(1+i\times n\right)[/latex]
Where:
- FV = value of investment at the end of period n
- PV = original principal (P0) or present value
- i = the rate of interest per period
- n = the number of periods
2.3.2 Future value and compounding frequency
Compounding frequency refers to how often the interest on an investment or loan is calculated and added to the principal balance. This frequency can significantly impact the amount of interest accrued over time. The more frequently interest is compounded, the more interest is earned on the interest already accumulated. Common compounding frequencies include:
Annual compounding: Interest is compounded once a year. This is the simplest form of compounding. For example, with an annual interest rate of 5%, $100 compounded annually would grow to $105 after one year.
Semi-annual compounding: Interest is compounded twice a year. Interest is paid and added to the principal two times per year. The interest rate per period is the annual interest rate divided by two since it is the rate that is applied every six months.
For example, with an annual rate of 6%, a principal of $100 would earn 3% interest (half of 6%) in the first six months, and then the new amount ($103) would earn another 3% for the second half of the year.
Quarterly compounding: Interest is compounded four times a year. The annual rate is divided by four, and this rate is applied every quarter.
Monthly compounding: Interest is compounded every month. The annual rate is divided by 12, and this monthly rate is applied to the balance each month.
The formula for compound interest considering different compounding frequencies is:
Equation 3:
[latex]{\rm FV}_n=PV×\left(1+i/m\right)^{m*n}[/latex]
Where:
- m = Number of compounding periods in a year
- n = Number of years in the entire period
Example: You have $1,000 to invest in a bank account paying an interest of 5% p.a. What is the value of your investment after 10 years if interest is compounded annually, semi-annually, quarterly and monthly.
Answer: i = 0.05, with annual compounding, m = 1, m x n = 10 x 1 =10. The above formula yields a future value of $1,628.89. For semi-annual compounding, the future value is $1,638.62 (m = 2, m x n = 20, i = 0.05/2 = 0.025). Similarly, the future value under quarterly and monthly compounding is $1,643.62 and $1,647.01, respectively. This example demonstrates how more frequent compounding can lead to greater accumulation of wealth due to the "interest on interest" effect.
In fact, the above formula and the one in equation 2 are equivalent. I is the interest rate per period and n is the number of periods. If nominal interest is 5% p.a but compounding every quarterly then the interest per period is 5%/4 = 1.25%. If the investment horizon is 10 years but interest payment is calculated every quarter then the number of periods in quarters is 40. Note that i and n has to match. If interest is on a per quarter period, the number of periods should also be the number of quarters.
2.3.3 Present value and discounting
The future value is calculated by determining how much the present value will grow to over a certain period. Conversely, the present value is calculated by determining how much a future amount of money worths in terms of today’s dollars. The method of converting the future value back to the present is called discounting. In other words, the present value is the discounted value of future cash flows.
Present value can be calculated using equation 4:
Equation 4:
[latex]PV=\frac{{FV}_n}{\left(1+i\right)^n}[/latex]
The formula illustrates that as n increases, PV decreases. The value a dollar in the future decreases if it is received later in the future. The higher the discount rate i, the lower the present value. The discount rates reflect the opportunity cost of capital i.e. the potential return that investors forgo when they choose to invest their resources in one option over an alternative. It is the rate of return the investor could have earned by putting his/her money into the next best investment. Therefore, the higher the discount rate, the less valuable a future dollar is today as investors prefer to receive money sooner rather than later if they can earn a higher return on that money elsewhere.
Example: You're planning a vacation in five years and anticipate it will cost $10,000. Given a 5% annual interest rate from the bank, how much should you deposit now to ensure you have the $10,000 needed for the trip in five years?
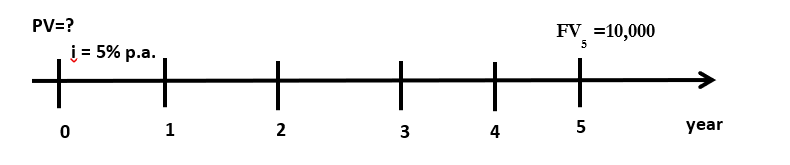 Answer: Applying equation 5, where FV5 = $10,000; i= 0.05, n=5.
Answer: Applying equation 5, where FV5 = $10,000; i= 0.05, n=5.
Equation 5:
[latex]V=\frac{{FV}_n}{\left(1+i\right)^n}[/latex]
[latex]=\frac{10,000}{\left(1+0.05\right)^5}=\frac{10,000}{1.27628}=$7,835[/latex]
So, you need to deposit $7,835 into the bank now in order to receive $10,000 in 5 years.
2.3.4 Other applications
Due to the time value of money, cash flows at different times cannot be simply summed up in their nominal amounts. To compare or aggregate them, they must be adjusted to a common point in time, either through discounting to present value or compounding to a future value. For example, if you receive $100 today and another $100 in a year, you can't just add them to say you have $200 at today's value. If the annual interest rate is 5%, the $100 received a year later is actually worth less today. Using discounting, its present value would be around $95.24. So, in today's terms, you would have $195.24, not $200.
From equation 2, if you know future value, interest rate and time periods, you can work out present value. In generally, knowing any three variables will enable you to figure out the fourth one. For example, in 2012, Facebook (now Meta) went public with the price of $38 per share. In 2024, the current price of Meta is $374 per share. What is the annual rate of return did the investors who bought the shares at $38 at the IPO and hold them until January 2024?
Answer: Applying the formula in equation 2 where FV = $374, PV = $38, n = 12. The missing variable is r. $374 = $38 * (1 +r)12. (1+r)12 =374/38 = 9.8421. (1+ r) = 9.84211/12
R= 1.2099 – 1= 20.99% or 21% per year.
2.4 Annual percentage rate versus effective annual rate
Interest rates in financial markets can be presented in several forms, with the Annual Percentage Rate (APR) being the most common, particularly when dealing with banks. The APR is based on the assumption of once-a-year compounding. However, this doesn't truly reflect the 'effective' interest rate if we're evaluating loan terms that compound more frequently.
The more precise way to gauge the yearly rate, accounting for the impact of multiple compounding periods within the year, is to use the Effective Annual Rate (EAR). The EAR is essentially the actual yearly growth rate that includes the effects of compounding. This rate provides a genuine measure of the cost associated with borrowing or the real yield from lending when compounding is more frequent than annually.
For example, if a bank quotes an APR of 6% with semi-annual compounding, the EAR would be higher than 6% because the interest is compounded twice a year, not once. To calculate the EAR from the APR in this scenario, you would use the formula to adjust for the effect of compounding. The calculation would show that the EAR is approximately 6.09%, which is the true cost of the loan or the actual yield on an investment over the year, taking into account the compounding effect.
Equation 6: Effective annual rate formula
[latex]EAR={(1+\frac{quoted\ annual\ interest\ rate}{m})}^m\ -1 = {(1+\frac{i}{m})}^m\ -1[/latex]
M is the frequency of compounding periods within a single year, indicating how often interest is calculated and added to the balance over that year. Effective Annual Rate (EAR) provides a more precise measure of the annual interest rate, factoring in the effects of the compounding periods.
Example: Suppose your mortgage comes with a stated annual interest rate of 8% per annum; however, the repayments are structured on a monthly basis. You'd want to know the actual yearly interest rate the bank is effectively applying to your loan. This is determined by calculating the Effective Annual Rate (EAR), which takes into account the monthly compounding of interest.
Applying the above formula where m = 12, APR = 8%, so the monthly interest rate is 8%
[latex]\mathrm{Monthly\ Rate\ =\ }\frac{0.08%}{12}=0.006667[/latex]
[latex]EAR=(1+Monthly)^{12}-1[/latex]
[latex]=\left(1+0.006667\right)^{12}-1[/latex]
[latex]=8.3%[/latex]
Quoted versus effective annual interest rate:
| Frequency | Quoted Annual Rate | n | Formula | Effective Annual Rate |
| Annual | 10% | 1 | I | 10% |
| Semi-annual | 10% | 2 | (1+i/2)2-1 | 10.25% |
| Monthly | 10% | 12 | (1+i/12)12-1 | 10.47% |
| Daily | 10% | 365 | (1+i/365)365-1 | 10.5156% |
| Continuous | 10% | ∞ | ei-1 | 10.5171% |
Continuous compounding is used in other more advanced finance subjects (such as derivatives).
Takeaways and looking ahead
In this chapter, we define and describe the implications of the time value of money. We also explore the process of compounding and discounting. Finally, we distinguish between the stated (nominal) annual interest rates, which do not take into account the frequency of compounding within a year, and effective annual interest rates which do reflect compounding effects, thereby offering a true reflection of the annual interest rate.
References:
Graham, J., Smart, S. B., Adam, C., Gunasingham, B. Introduction to Corporate Finance (2nd Asia – Pacific Edition) 2017.
Brealey, R., Myers S. C., Allen F., Edmans, A. Principles of Corporate Finance (14th Edition) 2022.
Peirson, G., Brown, R., Easton, S., Howard, P., Pinder, S. Business Finance (12th Edition) 2015.

