Chapter 5 – Bond market and bond valuation
Chapter Learning Objectives
After completing this chapter, students should be able to
- Understand the fundamental principles of bonds and the bond market.
- Compute the price of a bond and explain the relation between bond prices and interest rate.
- Distinguish between a bond’s coupon rate and yield to maturity.
- Explain the concept of interest rate risk, default risk and default risk premium
5.1. What is a bond?
A bond is essentially a form of debt instrument, which can be likened to an "I owe you" note. It represents a formal and enforceable contract between the issuer, who is the borrower, and the investor, who acts as the lender. This agreement outlines several key components:
- Par value: This is also known as the face value or principal of the bond. It is the amount that the issuer agrees to repay the bondholder at the bond's maturity.
- Coupon rate: The coupon rate is the interest rate that the bond issuer pays on the bond's face value. It is usually a fixed percentage, expressed as an annual percentage rate (APR). However, there can be variable or floating rates, which are often linked to benchmarks like the LIBOR or inflation indicators.
- Coupon payment dates: These are the scheduled dates on which the bond issuer makes interest payments to the bondholder. The payments are typically made on a quarterly or semi-annual basis.
- Maturity date: This is the date on which the bond will expire, and the issuer is obligated to pay the par value to the bondholder. Bonds can have varying lengths of maturity, ranging from a few months to several decades.
In the context of bonds, the issuer does not need to know the identity of the bondholder. The bond issuer has a legal obligation to make payments, such as interest or principal repayments, to whom-ever is in possession of the bonds at the time those payments are due. This means that if the bonds are sold or transferred from one investor to another, the issuer's responsibility is to make the due payments to the new holder of the bonds. This anonymous nature of bond ownership allows for easy trading of the bonds on the market, as the transfer of ownership does not require the issuer’s direct involvement or notification.
5.1.1 Types of corporate bonds
- Coupon bonds: are a type of bond that feature fixed interest payments, known as coupons, which are paid to the bondholder periodically over the bond's lifespan. The rate of these coupon payments is predetermined and remains constant until the bond reaches its maturity date. Upon maturity, the principal amount of the bond is repaid to the bondholder, and the bond is then considered retired or concluded. Coupon bonds often include standard call provisions that are common in many types of bonds. This provision gives the issuer the right, but not the obligation, to pay back the face value of the bond before its maturity date under specific conditions. This can be beneficial for the issuer, particularly if interest rates have fallen since the bond was issued, allowing them to refinance at a lower cost. Coupon payments are often made on an annual or semi-annual basis.
- Zero coupon bonds: are bonds that do not offer periodic coupon payments. Instead, investors receive a single payment at the bond’s maturity. Since zero-coupon bonds do not provide coupon or interest payments, they are typically sold at a significant discount from their face (or par) value. The difference between the par value and price of the bond represents the interest that accumulates over the life of the bond.
- Convertible bonds: are bonds that offer the bondholder the right to convert the bond into a predetermined number of shares of the issuing company's common stock at specific times during the bond's life, usually at the discretion of the bondholder.
5.1.2 Overview of Australian financial market
Have a look at the Figure 1: Australian Financial Markets on this Australian Equity Market Facts page on the RBA website. This depicts the types and historical trends of various financial securities in Australia as a percentage of GDP, indicating their relative size and importance within the economy over time.
The graph depicts a contrasting trend between government bonds and equities. While the proportion of government bonds relative to GDP has generally decreased, the equity market has shown growth, particularly from the 1980s onwards. Corporate bonds have also grown but remain a smaller fraction of the GDP compared to equities and government bonds. Overall, there is a general shift in the Australian financial markets from a strong reliance on government and government-backed bonds in the early 20th century towards a more diversified structure with significant equity and corporate bond markets in the later years.
5.2 Coupon rate versus coupon yield
The bond contract often states the coupon rate and other features of the bond such as par value, time maturity or whether or not the bond is callable. However, it does not specifies the yield to maturity i.e. coupon yield, another variable that determines the price of the bond. So, what is yield to maturity and how it differs from the coupon rate?
Coupon rate determines the annual interest rate that the issuer promises to pay the bondholder on the bond's face value, expressed as a percentage.
[latex]Coupon\ rate = \frac{Annual\ coupon}{Par\ value}[/latex]
Coupon yield: is the return that an investor can expect to receive from the bond if it is held until maturity assuming all the coupon payments are reinvested at the same rate.
[latex]Coupon\ yield = \frac{Annual\ coupon}{Bond\ price}[/latex]
While coupon rate is often fixed, the coupon yield can change over time if the price of the bond changes due to market conditions.
5.3 Bond Valuation
5.3.1 The valuation principle
The value of a financial asset is equal to the present value of all expected future cash flows, discounted at an appropriate discount rate
Equation 1:
[latex]P = \frac{CF_1}{(1+i)^1} + \frac{CF_2}{(1+i)^2} + \frac{CF_3}{(1+i)^3} + \cdots + \frac{CF_n}{(1+i)^n}[/latex]
Where:
- P = Value (price) of an asset at time 0, present value of the stream of cash flows
- CFt = cash flow in period t
- i = the market interest rate (discount rate)
- n = number of discounting periods
Based on this formula, the value or price of any financial asset at time 0 can be calculated by forecasting the future cash flows the asset is expected to generate and then discounting these cash flows to their present value using an appropriate discount rate. Let’s apply this valuation principle to price a coupon paying bond.
5.3.2 Bond valuation
For a coupon paying bond, the cash flows comprise two components: the coupon payments and the par value component usually paid at the maturity date. The timeline of the cashflows for a coupon bond is depicted as follows:

Given that the coupon payments remain constant and the first payment is made one period after time 0, this series of coupon payments essentially constitutes an ordinary annuity. Consequently, we can apply the present value formula for an ordinary annuity to calculate the current worth of these coupon payments at time 0.
The second component is the par value, the lumpsum that usually paid at maturity. Since it is a one-off payment, we can use the formula for single cash flow to discount it back to present. The price of the bond is the PV of coupons + PV of par value.
Equation 2:
[latex]\ P_B = \frac{C}{(1+i)^1} + \frac{C}{(1+i)^2} + \frac{C}{(1+i)^3} + \cdots + \frac{C}{(1+i)^n} + \frac{F_n}{(1+i)^n}[/latex]
The price of the bond then becomes PV of an ordinary annuity + PV of one last single cash flow (or Par value)
Equation 3:
[latex]P_B=\frac{C}{i}×[/latex][latex]\left[1-\frac{1}{\left(1+i\right)^n}\right]+\frac{F_n}{\left(1+i\right)^n}[/latex]
where Fn is the par value.
Example: AR Ltd is issuing a 10-year bond with a coupon rate of 8.89 per cent. The interest rate for similar bonds is currently 5.97 per cent. Assuming annual payments and a face value of $1000, what is the present value of the bond?
Answer: Step 1: Outline the cash flows that the financial asset i.e. the bond pays. The coupon payment each period is:
Coupon payment per period = [latex]\frac{\mathrm{annual\ coupon\ rate\ x Par\ value}}{\mathrm{number\ of\ coupon\ payment\ in\ a\ year}}[/latex]
= [latex]\frac{\mathrm{0.0889\times1000}}{1}\mathrm{=$88.9}[/latex]
So, the cashflows are: 88.9 per year for 10 years and a one-off 1000 at the end of year 10. N = 10 and i = 0.0597. The discount rate is the coupon yield. It reflects the opportunity cost of capital i.e. the return that investors expect from the bond.
[latex]P_B=\frac{C}{i}×[/latex][latex]\left[1-\frac{1}{\left(1+i\right)^n}\right]+\frac{F_n}{\left(1+i\right)^n}[/latex]
[latex]=\frac{88.9}{0.0597}\times\left[1-\frac{1}{{(1+0.0597)}^{10}}\right]+\frac{1000}{{(1+0.0597)}^{10}}[/latex]
[latex]=\ \frac{88.9}{0.0597}\times0.4400+559.9776[/latex]
[latex]=655.2094+559.9776[/latex]
[latex]=$1215.19[/latex]
5.3.3 Par, premium and discount bonds
- Par bonds: When a bond's coupon rate (C) is equal to the market rate (i), the bond will trade at its face (or par) value. The reason is the market rate i.e. yield to maturity represent the rate of return that investors expect from holding the bond. If investors expect a rate of return of 10% p.a for holding the bond and the coupon rate is also exactly 10%, the bond will be selling at par.
- Discount bond: If the coupon rate (C) of a bond is lower than the prevailing market interest rate (i), the bond will be sold at a price below its face (or par) value. The reason is the coupon rate that the bond is offering is less than what investors expect. Therefore, to achieve the required rate of the return, investors will sell the bond driving its price below the par value.
- Premium bonds: When a bond's coupon rate (C) exceeds the current market interest rate (i), the bond will be traded at a price higher than its face (or par) value. In this case, the coupon rate that the bond is offering is higher than what investors expect which make investors willing to pay a price that is higher than the par value.
5.3.4 Semi-annual bond valuation
Most corporate bonds make coupon payments semi-annually, meaning twice a year. However, it's a standard practice to quote their coupon rates on an annual basis. This means that even though these bonds pay coupons every six months, the stated coupon rate reflects the interest amount that would be paid over a full year. For instance, if a bond has an annual coupon rate of 4%, it would actually pay 2% every six months. The formula for a semi-annual coupon paying bond is as follows:
Equation 4:
[latex]P_B=\frac{C/2}{i/2}×\left[1-\frac{1}{\left(1+i/2\right)^{2n}}\right]+\frac{F_{2n}}{\left(1+i/2\right)^{2n}}[/latex]
Since the coupon payment is made every six months if the bond matures in n years, in total, there would be 2n periods. is the par or face value paid in period 2n.
Example: You are interested in investing in a 3-year bond with a face value of $1000 that pays a 6.3 per cent coupon with interest to be received semi-annually. Your required rate of return is 6.6 per cent. What is the most that you would be willing to pay for this bond?
Answer: The coupon rate is 6.3% p.a, since the coupon is paid every six months. The coupon payment each period is 0.063×1000/2 = 31.50. The number of periods is therefore 3x2 = 6. The discount rate each period is 0.066/2 = 0.033 since each period is now 6 months instead of 1 year.
[latex]P_B=\frac{C/2}{i/2}×\left[1-\frac{1}{\left(1+i/2\right)^{2n}}\right]+\frac{F_{2n}}{\left(1+i/2\right)^{2n}}[/latex]
[latex]\mathrm{=}\frac{\mathrm{63/2}}{\mathrm{0.066/2}}\mathrm{\times}\left[\mathrm{1}-\frac{\mathrm{1}}{{\mathrm{(1+0.066/2)}}^{\mathrm{2*3}}}\right]\mathrm{+}1000(1+0.066/2)2*3[/latex]
[latex]\mathrm{=954.5455} \mathrm{\times}\left(\mathrm{1-0.823}\right)\mathrm{+822.9967}[/latex]
[latex]\mathrm{=168.9546+822.9967}[/latex]
[latex]\mathrm{$991.9513}[/latex]
5.3.5 Zero coupon bond
As the name implied, zero coupon bond has no coupon payment. The only cash flow that the bond pays is the par value. The value of the bond is simply the present value of this final cash flow discounted back to the present using the appropriate discount rate i.e. yield to maturity.
Equation 5:
[latex]P_B = \frac{F_n}{(1+i)^n}[/latex]
Example: You are thinking to invest in a zero coupon bond that is matures in 6 years with a face value $100,000. How much are you willing to pay for the bond if the current market interest rate for similar bond is 6% p.a?
Answer: Par value is $100,000, n=6 and yield to maturity I = 0.06.
[latex]P_B = \frac{1000}{(1+0.06)^6} = \$79,406.05[/latex]
5.4 Bond yields
Yield to maturity (YTM): is the rate of return that an investor expects to earn if they hold a bond until its maturity date, and all scheduled coupon and principal payments are made without default. It is used as a discount rate that makes the present value of coupons and principal payments equal to the price of the bond. YTM is not static, it changes in response to changes in market interest rates and other economic factors.
When market interest rates rise, investors expect a higher return from their investments which lead the YTM of existing bonds increases, often resulting in lower bond prices. Conversely, when market interest rates fall, the YTM of existing bonds generally decreases, leading to higher bond prices. This inverse relationship between yield and price is a fundamental principle of bond investing.
Bonds with longer maturities experience greater price fluctuations compared to bonds with shorter maturities for the same level of change in their Yield to Maturity (YTM).
For bonds valuation, since the cash flows are predetermined, the price of the bond largely depends solely on the discount rate (YTM). How do we know what investors required rate of return on a bond is?
Answer: We can invert the yield to maturity from the bond price and once the YTM is obtained, it will enable us to price similar bonds.
Example: Westpac Banking Corporation has a 3-year bond outstanding that pays a 7 per cent coupon and is currently priced at $913.88. What is the yield to maturity of this bond? Assume semi-annual coupon payments and a par value of $1000.
Answer: Since the coupon is paid semi-annual, the number of periods is 2 x 3 =6. The coupon payment each period is 0.07 x 1000 = 35.
Applying formula in equation 4:
[latex]\mathrm{913.88=}\frac{\mathrm{70/2}}{\mathrm{i/2}}\mathrm{\times}\left[\mathrm{1-}\frac{\mathrm{1}}{{\mathrm{(1+i/2)}}^{\mathrm{2*3}}}\right]\mathrm{+}1000(1+i/2)2*3[/latex]
[latex]\mathrm{13.88=}\frac{\mathrm{35}}{\mathrm{y}}\mathrm{\times}\left[\mathrm{1-}\frac{\mathrm{1}}{{\mathrm{(1+y)}}^\mathrm{6}}\right]\mathrm{+}1000(1+y)6[/latex]
Y denotes yield to maturity or i in equation 4.
Using excel, y = 5.21% so i = 2 x y = 2 x 5.21% = 10.42%.
5.5 Risk of investing in bonds
Investing in bonds, like any other investments involves a number of risks. The two major risks that associated with bonds are:
- Credit (Default Risk): This risk reflects the probability that the bond issuer will be unable to fulfill the debt payment obligations as they fall due. Generally, government bonds have lower credit risks compared to corporate bonds. Credit rating agencies assign ratings to bonds globally, serving as an indicator of their credit risk. These ratings essentially evaluate the likelihood that the bond issuer will default on its debt obligations, including interest payments and the repayment of the principal. A higher rating suggests a lower risk of default, indicating greater financial stability and strength of the issuer. Conversely, a lower rating indicates higher risk, implying a greater chance that the issuer might fail to meet its payment obligations.
- Interest rate: Interest rate risk refers to the possibility of incurring losses on investments due to a rise in market interest rates. When interest rates in the market go up, the appeal of holding existing bonds diminishes. This is because new bonds issued in the market offer higher coupons compared to the fixed coupons of existing bonds.
5.5.1 Interest rate risk
When interest rates in the market rise, the Yield to Maturity (YTM) of bonds also increases. This is because YTM is essentially a reflection of the opportunity cost of capital. If interest rates are higher, investors naturally expect greater returns on their investments since they could potentially earn more by investing in other opportunities with higher yields. Consequently, as market interest rates go up, the required rate of return (or discount rate) for existing bonds increases, which in turn lowers their market prices.
The impact of rising interest rates on bond prices, however, is not uniform across all bonds. Generally, bonds with longer maturities are more sensitive to changes in interest rates and will experience greater price reductions compared to shorter-term bonds. This is because the longer the time until a bond's maturity, the longer the period during which the investor is locked into lower coupons relative to the market, thus increasing the bond's interest rate risk. The following picture compares the price of a 1-year bond and a 10-year bond when interest rate changes:
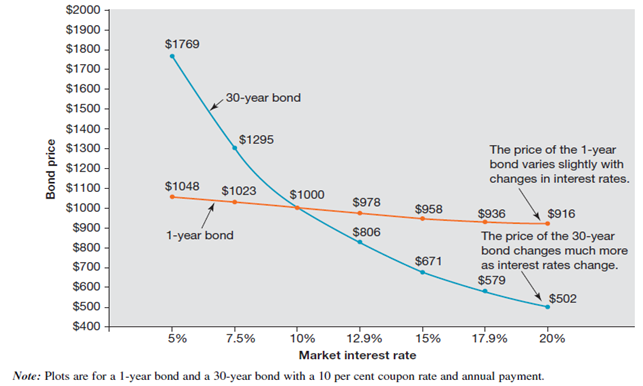
The graph demonstrates that when market interest rates increase, the prices of both short-term and long-term bonds decrease. However, the extent of the price decline differs significantly between the two. While the short-term bond experiences a relatively minor decrease in price, the long-term bond's price drops much more sharply.
5.5.2 Default risk
As mentioned above, default risk that borrowers may not make the promised payments. It is the risk of losing not just the return on capital but the return of capital i.e. the principal. Therefore, in order to hold bonds that have positive default risk, investors must be paid a premium. Default risk premium (DRP) is the difference between interest rate on a security that has default risk (idr) and the interest rate on a risk-free (irf) security.
DRP = idr – irf
The DRP is essentially the extra return that a bond offering a default risk pays over a risk-free security, like an Australian Government Bond.
5.5.3 Bond ratings
Moody's Investors Service (Moody's) and Standard & Poor's Global Ratings (S&P) are the two leading credit rating agencies that evaluate the likelihood of borrowers repaying their debts, effectively assessing their creditworthiness. Fitch Group ranks as the third largest in this field. While Moody's and S&P have their own unique rating scales, the meaning behind their ratings is broadly similar.
The highest quality bonds, considered to have the minimal risk of default, are given the top ratings of Aaa by Moody's and AAA by S&P. These ratings reflect the highest level of creditworthiness.
Bonds are categorized as investment-grade if they are rated between Aaa (or AAA) and Baa (or BBB). These ratings suggest a lower risk of default and are typically sought after by conservative investors, including certain institutional investors.
Conversely, bonds rated below Baa (or BBB) are classified as non-investment grade. These include junk bonds, speculative-grade bonds, or high-yield bonds, which carry a higher risk of default but offer higher returns to compensate for this increased risk.
The following table shows the Investment ratings by S & P, Moody and Fitch:
| S & P | Moody | Fitch | Description | |
| Investment Grade | ||||
| AAA | AAA | Aaa | AAA | Prime, highest quality, lowest credit risk |
| AA+ | AA+ | Aa1 | AA+ | High quality, very low credit risk |
| AA | AA | Aa2 | AA | |
| AA- | AA- | Aa3 | AA- | |
| A+ | A+ | A1 | A+ | Upper medium grade, low credit risk |
| A | A | A2 | A | |
| A- | A- | A3 | A- | |
| BBB+ | BBB+ | Baa1 | BBB+ | Lower medium grade, moderate credit risk |
| BBB | BBB | Baa2 | BBB | |
| BBB- | BBB- | Baa3 | BBB- | |
| Non-investment grade (Junk) | ||||
| BB+ | BB+ | Ba1 | BB+ | Speculative, substantial credit risk |
| BB | BB | Ba2 | BB | |
| BB- | BB- | Ba3 | BB- | |
| B+ | B+ | B1 | B+ | Highly speculative, high credit risk |
| B | B | B2 | B | |
| B- | B- | B3 | B- | |
| CCC+ | CCC+ | Caa1 | CCC | Substantial risks, extremely speculative |
| CCC | CCC | Caa2 | CCC | |
| CCC- | CCC- | Caa3 | CCC- | |
| CC | CC | Ca | CC | |
| C | C | C | C | Extremely high levels of credit risk |
| D | D | D | Default |
5.5.4 Australian bond market
In Australia, most corporate bonds are not traded on the Australian Securities Exchange (ASX), the primary stock exchange in the country. Instead, these bonds are typically traded over-the-counter (OTC). OTC trading means that the bonds are traded in a decentralized manner, often through broker-dealer networks, rather than on a centralized exchange like the ASX. To invest in these corporate bonds, an investor usually needs to go through a broker. The broker executes the order by finding a matching buyer or seller in the OTC market. This method of trading can be less transparent than exchange trading, with prices and availability varying more significantly.
For individual investors looking to invest in bonds through a more familiar and accessible platform, Exchange-traded Treasury Bonds (eTBs) offer an alternative. eTBs are essentially government bonds that are listed and traded on the ASX. They represent an investment in an Australian Government bond, providing the safety and stability associated with government debt. These bonds are more accessible to individual investors and offer benefits like regular interest payments and the return of face value at maturity. eTBs can be bought and sold just like stocks through the ASX, offering transparency, ease of trading, and accessibility that might not be available with OTC corporate bonds.
Takeaways and looking ahead
This chapter provided an overview of bonds and the Australian bond market, detailing how bonds function as a crucial method for companies and other entities to raise capital. As debt securities, bonds involve lending money to the issuer in exchange for regular interest payments and the return of the principal at maturity. We've explored the various aspects of bonds, including their pricing, the relationship between bond prices and interest rates, the distinction between a bond's coupon rate and its yield to maturity, and the risks associated with bond investing, such as interest rate risk and default risk.
In the next chapter, we will shift our focus to the second major channel for companies to raise capital: equity. Equity represents ownership in a company and comes with different characteristics and valuation methods compared to debt securities like bonds. We will explore the different types of equity securities, and the principles behind equity valuation. This will provide a comprehensive understanding of how companies raise capital and how investors can evaluate and invest in these different types of securities
References:
Graham, J., Smart, S. B., Adam, C., Gunasingham, B. Introduction to Corporate Finance (2nd Asia – Pacific Edition) 2017.
Brealey, R., Myers S. C., Allen F., Edmans, A. Principles of Corporate Finance (14th Edition) 2022.
Peirson, G., Brown, R., Easton, S., Howard, P., Pinder, S. Business Finance (12th Edition) 2015.

